This is an introduction to the way EMT handles matrices for linear algebra. You should be familiar with the Euler matrix language by now.
Let us start with a simple matrix.
>A:=[1,2,3;4,5,6;7,8,9]
1 2 3
4 5 6
7 8 9
det() computes the determinant, which surprisingly is 0 for this matrix.
>det(A)
0
Consequently, the kernel of A will contain non-zeros elements.
>kernel(A)
1
-2
1
Let us check, using the dot product.
>A.kernel(A)
0
0
0
By the way, the matrix language provides a very simple way to produce this matrix. We generate the vector 1:9, and put its entries into the rows of a 3x3 matrix.
>redim(1:9,3,3)
1 2 3
4 5 6
7 8 9
Now we try to solve a linear system.
>b:=[3;4;3]
3
4
3
This fails, since the matrix is singular.
>x:=A\b
Determinant zero!
Error in:
x:=A\b ...
^
Singularity is checked with the internal epsilon. In this case, the numerical solver recognizes that the matrix is singular.
EMT has another solver, which applies the pseudo-inverse of A to b. The solution is the best possible in distance with least norm. But it is not a proper solution.
>x:=svdsolve(A,b); fracprint(x)
-5/3
0
5/3
The error is still substantial, but it is the smallest possible error, nevertheless.
>norm(A.x-b)
0.816496580928
This is as close as we can get to b.
>A.x
3.33333
3.33333
3.33333
The fit function finds another solution with the same error. It is a bit faster.
>x:=fit(A,b); fracprint(x), norm(A.x-b)
-10/3
10/3
0
0.816496580928
We change one element of A.
>A[3,3]:=0
1 2 3
4 5 6
7 8 0
Now, A is regular.
>det(A)
27
And we can properly solve the linear system.
>x:=A\b; fraction x
-19/9
20/9
2/9
Indeed, this is the solution.
>norm(A.x-b)
0
Let us try a larger problem. We generate a 100x100 random matrix.
>A:=normal(100,100);
The determinant is huge.
>det(A)
-1.80259873511e+078
We multiply with a random vector.
>x:=random(rows(A),1); b=A.x;
The norm of the error is usually quite good. We need to switch to longestformat to avoid the error being rounded to 0 for the output.
>longest norm(A\b-x)
8.661666511000772e-014
In the following commands we demonstrate how to do the Gram-Schmid method by hand for the vectors v and w.
>v:=[1;1;1]; w:=[1;2;-1]; v1:=w-(w'.v)/(v'.v)*v; fracprint(v1);
1/3
4/3
-5/3
We could continue like this. But we take the cross product to get the third vector.
>v2:=crossproduct(v,w),
-3
2
1
Now, the normalized vectors v, v1, v2 should form an orthogonal matrix.
>M:=[v/norm(v),v1/norm(v1),v2/norm(v2)]
0.57735 0.154303 -0.801784
0.57735 0.617213 0.534522
0.57735 -0.771517 0.267261
Let us check this.
>norm(M.M'-id(3))
0
We can directly expand v to an orthonormal basis. For this, we note the space kernel(A') is orthogonal to all columns of a matrix A. Then we apply the utility function orthogonal() to all vectors.
>orthogonal(v|kernel(v'))
0.57735 -0.707107 -0.408248
0.57735 0.707107 -0.408248
0.57735 0 0.816497
Let us project the vector b to the plane generated by v and w. The coefficients of v and w minimize l1*v1+l2*v2-b.
The function "fit" does just this projection.
>A:=v|w; b:=[1;0;0]; l:=fit(A,b); fracprint(l);
2/7
1/14
We can compute the projection A.l.
>z:=A.l; fracprint(z);
5/14
3/7
3/14
And we compute the distance of z to this plane.
>norm(z-b)
0.801783725737
We could also use our matrix M to get the same result. The first two columns span the plane and are orthonormal.
>l:=M'.b; l=l[[1,2]]; M[:,[1,2]].l
0.357143
0.428571
0.214286
Another idea is to use the projection to v2. The matrix of this projection is v2.v2', after v2 is normed to 1.
>P:=id(3)-v2.v2'/norm(v2)^2; P.b
0.357143
0.428571
0.214286
Maxima knows a lot of functions for linear Algebra too. We can define the Matrix as data for symbolic expressions.
>A &:= [1,2,3;4,5,6;7,8,9]
1 2 3
4 5 6
7 8 9
The rank of the matrix is 2, because it is singular.
>&rank(A)
2
The result of the Gauss algorithm applied to A can be computed with echelon.
The echelon form can be used to determine a base of the lines of A taking the non-zero lines of A. Moreover, the independent columns of the echelon form, are the columns of A, which form a basis of the columns of A.
>&echelon(A)
[ 1 2 3 ]
[ ]
[ 0 1 2 ]
[ ]
[ 0 0 0 ]
Here is one way to make a linear system from the matrix A, and to solve it. The system is A.[x,y,z]=[1,1,1].
>&transpose(A.[x,y,z]-[1,1,1]), sol &= solve(%[1],[x,y,z])
[ 3 z + 2 y + x - 1 6 z + 5 y + 4 x - 1 9 z + 8 y + 7 x - 1 ]
[[x = %r1 - 1, y = 1 - 2 %r1, z = %r1]]
The list of symbols is contained in a temporary list named %rnum_list, which we can access with temp(1). We can assign a value for each symbol as follows.
>&sol with temp(1)=0
[[x = - 1, y = 1, z = 0]]
For an invertible matrix, there is also a function lusolve(), which directly solves Ax=b.
>&lusolve([1,2,3;4,5,6;7,9,10],[1;1;1])
[ 0 ]
[ ]
[ - 1 ]
[ ]
[ 1 ]
With Maxima, we can use symbolic matrices containing variables or other expressions.
>A &= [1,2,3;4,5,6;7,8,a]
[ 1 2 3 ]
[ ]
[ 4 5 6 ]
[ ]
[ 7 8 a ]
We can easily see, that a=9 makes a singular matrix.
>&determinant(A)|factor
- 3 (a - 9)
We can now invert this matrix symbolically. This works unless the determinant is 0.
>Ainv &= ratsimp(inv(A)*det(A))
[ 5 a - 48 24 - 2 a - 3 ]
[ ]
[ 42 - 4 a a - 21 6 ]
[ ]
[ - 3 6 - 3 ]
We can print this with latex using the comment line "maxima: Ainv"
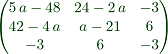
Let us do some eigenvalue problems.
First we generate a diagonal matrix of size 3x3, with the specified values on the 0-th diagonal.
>D:=diagmatrix([1,2,3])
1 0 0
0 2 0
0 0 3
We generate a random matrix similar to the matrix A.
>M:=random(3,3); A:=M.D.inv(M)
5.61971 3.54267 -5.38696
5.63576 6.88812 -8.29591
5.76664 5.13393 -6.50783
Indeed, the eigenvalues of A are just 1,2,3. However, we get complex eigenvalues, which need to make real.
>real(eigenvalues(A))
[3, 1, 2]
We can also use the function eigen() to compute both the eigenvalues and the eigenspaces.
>{l,v}:=eigen(A); real(v),
-0.863456 0.292455 1
-0.882092 1 0.108208
-1 0.908439 0.743101
Then inv(v).A.v should be the diagonal matrix of eigenvalues.
>norm(inv(v).A.v-diagmatrix(l))
0
Euler can also do singular value decompositions.
>{p,s,q}:=svd(A); s
[17.8852, 1.79654, 0.186732]
These are the eigenvalues of A'.A, but Euler uses a special algorithm for this.
>sqrt(abs(eigenvalues(A'.A)))
[17.8852, 1.79654, 0.186732]
We get A as a composition of two orthogonal matrices, and a diagonal matrix.
>norm(p.diagmatrix(s).q'-A)
0
Let us demonstrate, how to solve a linear system by hand. Assume, we have the following system.
>fracformat(10); A:=redim(1:12,3,4)
1 2 3 4
5 6 7 8
9 10 11 12
>pivotize(A,1,1)
1 2 3 4
0 -4 -8 -12
0 -8 -16 -24
>pivotize(A,3,2)
1 0 -1 -2
0 0 0 0
0 1 2 3
>swapRows(A,2,3)
1 0 -1 -2
0 1 2 3
0 0 0 0
There is the function echelon, which does all this automatically.
>fracformat(10); A:=redim(1:12,3,4); echelon(A)
1 0 -1 -2
0 1 2 3
We can also compute eigenvalues with Maxima. The function returns the eigenvalues and their multiplicities.
>longformat; A&:=[1,2;3,4]
1 2
3 4
>&eigenvalues(A)
5 - sqrt(33) sqrt(33) + 5
[[------------, ------------], [1, 1]]
2 2
Here are the eigenvectors.
>&eigenvectors(A)
5 - sqrt(33) sqrt(33) + 5
[[[------------, ------------], [1, 1]],
2 2
3 - sqrt(33) sqrt(33) + 3
[[[1, ------------]], [[1, ------------]]]]
4 4
Euler has a special data types, and algorithms for large and sparse system. For more information refer to the following introduction.
The following does not use these algorithms, and the matrix is full. Yet, Euler can produce a good solution within seconds.
>A=normal(500,500); b=sum(A); x=A\b; >totalmax(A.x-b)
0