Euler supports Python as a scripting language. You need to install Python 2.7 for this. Other versions won't work, since Python wants to be linked against a specific version. The purpose of this interface is to
See the last section for internals on the Python interface. For a documentation about Python, see the
EMT is partly compatible to Python 3.8. You can enable that in the program options before using Python. Note that the downward compatibility from Python 3 to Python 2 is not guaranteed in Python. Moreover, the MatPlotlib an NumPy libraries generate a lot of troubles both in EMT and in Python. So the recommended version is still Python 2.7, and you can get a complete version by using the Anaconda interface.
Direct commands for Python start with ">>> " at the beginning of the command line (alternatively with ">py: ").
>>> print ('Hello World!')
Hello World!
Depending on your settings, you are asked if you want to allow the command.
Note that print() was a command in Python 2 and the brackets were not needed. To get a bit of compatibility I am using the brackets in this introduction.
For a multi-line command, we can use a multi-line in Euler.
>py: s=42 ... print (str(s)+" is the answer")
42 is the answer
Note that ">>" must not appear in the second line, and the second line must not be indented, unless Python needs an indentation.
In Python 2, you can also use
print s, "is the answer"
For longer sections with Python code, it is more convenient to use a function body in Euler. Then you can use the internal Euler editor to edit the command. Press F9 in the first line to start this editor. Or simply click into the body and edit the commands in the same way as you can edit an Euler function.
>function python ... s=0 for i in range(1,101): s+=i print(s) endfunction
5050
This is not a function, but rather a collection of commands for Python. It runs as soon as you exit the collection.
You can continue a line in Python by ending it with \. Then you can also indent.
>function python ... x=2.5 print(1+x+x**2/2+x**3/6+\ x**4/24) endfunction
10.856770833333332
Note the "**" for the power operator! Let us check the result.
>"1+x+x^2/2+x^3/6+x^4/24"(2.5)
10.8567708333
Python can also be called with the function python(). This function accepts a string or a vector of strings. It returns a string.
>python("print(34*56)")
1904
The command can be used in Euler functions.
>function ptest(n) := python("print(7**"+n+")"); ...
ptest(40)
6366805760909027985741435139224001
The python() function accepts a vector of strings. The strings will become command lines for Python.
>python(["v=range(1,101)","print('sum = '+(str)(sum(v)))"])
sum = 5050
The default output of Python does not print like it does in a Python shell.
>>> 7**8
To print the result you need to use the print() command.
>>> print(7**8)
5764801
A shortcut is a colon at the first position of the line. EMT will wrap the line into a print command in this case.
>>> : 7**8
5764801
It is possible to switch to Python mode.
>pythonmode on
Python mode is on
Then Python works as expected. For control structures you need to use multi-lines and indentation.
>def fak(m): ...
n=1 ...
for k in range(2,m+1): ...
n=n*k; ...
return n
>print(fak(20))
2432902008176640000
Again, the colon is replaced by the print command.
>: fak(50)
30414093201713378043612608166064768844377641568960512000000000000
Maxima lines work inside the Python mode.
>:: 50!
30414093201713378043612608166064768844377641568960512000000000000
A line starting with "euler " will call EMT to parse the result.
>euler 20!
2.43290200818e+18
>pythonmode off
Python mode is off
Beware!
Python cannot be interrupted. If you program an eternal loop, you need to close Euler. But you can allow the user to interrupt the program with the eumat.testkey() function. The module eumat is imported automatically.
The function eumat.dump() prints to the notebook immediately, while the print() function of Python prints at the end of the execution.
>function python ...
eumat.dump("Press any key to stop the loop!")
while True:
if eumat.testkey():
break;
endfunction
Press any key to stop the loop!
The easiest way to define a Python function is the following.
>function python f(x) ... return x**3-x endfunction
Again, remember that Python uses ** for the exponent. x^3 does not work!
You can call this function in Python, of course.
>>> : f(0.7)
-0.35700000000000004
The function can also be called in EMT just like an Euler function. It is essentially a function in Python, which is known in EMT, and can be used directly.
>f(0.7)
-0.357
One alternative is to use pycall(). This method can be used to call any function of Python and get the result back in EMT.
>pycall("f",0.7)
-0.357
There is a shortcut for this.
>py$f(0.7)
-0.357
Of course, a Python function can also be defined in a collection of Python commands in the following way.
>function python ...
def fib(n):
a,b=1,1
for i in range(3,n+1):
a,b=b,a+b
return b
endfunction
The function fib() defined in these commands is an iteration, which computes the n-th Fibonacci number.
Inside Python, the function will return the result in the long integer type of Python.
>py: print(fib(200))
280571172992510140037611932413038677189525
For Euler, this is converted to a real number.
>longest py$fib(200)
2.805711729925102e+41
Here is a function, which returns all Fibonacci numbers up to the n-th number in a vector.
>function python fib (n) ... ## Compute n Fibonacci numbers if n<=1: return [1] v=list(range(0,n)) v[0]=1.0 v[1]=1.0 for i in range(2,n): v[i]=v[i-1]+v[i-2] return v endfunction
In Python 3, you need to convert a range to a list. A range is no longer producing a list automatically to increase performance. That was different in Python 2.
Note that Python functions defined in this way can have a help line. Thus the status line and F1 will work.
>help fib
fib is a Python function. function fib (n) Entered from command line. Python function. Compute n Fibonacci numbers
>fib(10)
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
We can use the result like any other vector in Euler.
>n=100; k=1:n; plot2d(k,fib(n)^(1/k),>points):

You can define your own modules in separate files, and import them in Python. The path to look for files is sys.path in Python. EMT appends the current directory to this path.
>py: ... import mymod ... print(mymod.fac(10))
3628800
The content of the file is very simple.
>printfile("mymod.py")
def fac(n):
p=1;
for i in range(2,n+1):
p*=i
return p
Note that Python will compile the module, generating "mymod.pyc". Thus you need to make sure that the file is in a writable directory. Moreover, you need to be aware that Python will not reload an updated module.
To call the function directly, there is a special syntax py$... which contains the name of the module.
>py$mymod$fac(5)
120
This can also be used for Python modules like cmath.
>python("import cmath"); py$cmath$exp(1+I)
1.46869+2.28736i
To set a global variable in Python from a value in EMT, we use pyset().
>pyset("a",1:10);
This will yield in a vector of integers in Python, since all numbers in the vector can be converted to integers.
>>> print(a)
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Conversely, you can get the values of Python variables for EMT.
>python("v=list(range(1,11))"); pyget("v")
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
The following Python code does the simple Euler method for a differential equation.
>function python dgleuler(f,y0,a,b,h) ... t,y = a,y0 while t < b: t += h y += h * f(t,y) return y endfunction
We need a function f(x,y).
>function python ftest(x,y) ... return -2*x*y endfunction
To handle the function f to the method dgleuler(), we use "py$ftest".
>dgleuler("py$ftest",1,0,1,0.001)
0.367266206411
>exp(-1)
0.367879441171
In numerical functions of EMT, the function ftest() can be used just as any other EMT function.
>ode("ftest",[0,1],1)[-1]
0.367879441182
Python can also call Euler functions. The Python interface imports the module euler, so you can use it immediately. The method we need is euler.call.
For an example, we rewrite the example.
>function python dgleuler(f,y0,a,b,h) ... t,y = a,y0 while t < b: t += h y += h * eumat.call(f,t,y) return y endfunction
Now we define the function in Euler.
>function f1(t,y) := -2*t*y
We call the Euler function by name.
>dgleuler("f1",1,0,1,0.001)
0.367266206411
To test the speed of Python, we define the Fibonacci numbers in a very inefficient, recursive way. This is a famous example to measure function calls in a language.
>function python fibrekpy (n) ... if n<=2: return 1 return fibrekpy(n-1)+fibrekpy(n-2) endfunction
>tic; fibrekpy(25), toc;
75025 Used 0.014 seconds
In Euler, a similar function is considerably less speedy.
>function fibrekeu (n) ... if n<=2 then return 1.0 else return fibrekeu(n-1)+fibrekeu(n-2) endfunction
>tic; fibrekeu(25), toc;
75025 Used 0.132 seconds
We try the example of in the tutorial about compiled code.
>function python hofstadter (n) ... v=list(range(1,n+1)) v[0]=1 v[1]=1 for i in range(2,n): k=v[i-1] v[i]=v[k-1]+v[i-k] return v endfunction
The result is typically up 10 times slower than comparable C code, but can be 10 times faster then Euler.
>tic; v=hofstadter(2^20); toc;
Used 0.218 seconds
>i=1:512; plot2d(v[i]/i):
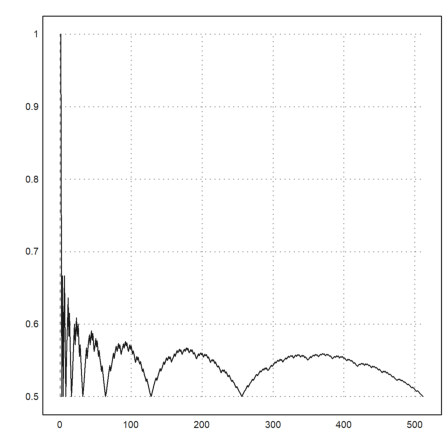
The next example loads the English word list of Euler to determine words, which are forward and backward in the list. These words are called "semordnilap" words (palindromes backwards).
The code is from the Rosetta page again.
>function python semordnilap (file) ...
with open(file) as f:
wordset = set(f.read().strip().split())
revlist = (''.join(word[::-1]) for word in wordset)
pairs = set((wrd, rev) for wrd, rev in zip(wordset, revlist)
if wrd < rev and rev in wordset)
w=list(pairs)
v=list(range(len(w)))
for i in range(len(w)):
v[i]=w[i][0]
return v
endfunction
We call this function and pass the filename as an argument.
>w=semordnilap(start()+"english.words"); length(w)
281
It returns a list of words, which is translated into a string vector. We print the first 5 words.
>w[1:5]
repins deer marcs gats pus
You can load Python files.
The following file contains code to solve a Hidako puzzle. I stole the code from
The load command will collect all output from the file, if it has any, and print the output. It is not designed for interactive programs.
>load hidako.py
Python is a script language with an own heap of variables. It runs externally as a subsystem in Euler, but Euler can start programs and functions in Python and get the results. Values are translated from Euler to Python and from Python to Euler.
The interface is contained in python.dll, which is loaded on demand. This library is linked to python27.dll, which runs the Python system. This is a safe approach, and it can be extended to new versions of Python later.
A command is sent directly to Python. The output is collected in a Python string, which is printed to the notebook at the end of the command. Python commands cannot be called in an interactive way.
>>> print("This is printed after the command finishes.")
This is printed after the command finishes.
Multi-line command and Python blocks behave in the same way. Since we sometimes what to print a string or a value immediately there is the function eumat.dump() in the module "eumat".
>function python ...
eumat.dump("Press any key!")
while True:
if eumat.testkey():
break;
endfunction
Press any key!
This function can print any data that EMT understands.
>py: eumat.dump(list(range(5)))
[0, 1, 2, 3, 4]
If functions are defined in Python they can be called in EMT with python("foo",..) or py$foo(...) as described above. For the process, parameters and results are translated between the systems.
Euler can transfer the following types:
If possible, double values are translated to integer values for Python.
>pyset("v",1:0.5:2); python("print(type(v[0]))")
<class 'int'>
Python vectors can contain a mix of integers and floats.
>py: print(v)
[1, 1.5, 2]
The eumat module is loaded at the start of the Python subsystem. It has the following functions
With call() many things are possible.
>function python plottest(n) ...
import random;
v=list(range(500));
for i in range(500):
v[i]=random.random()-0.5;
for i in range(1,500):
v[i]+=v[i-1]
eumat.call("plot2d",v)
eumat.call("insimg")
endfunction
>plottest(500)
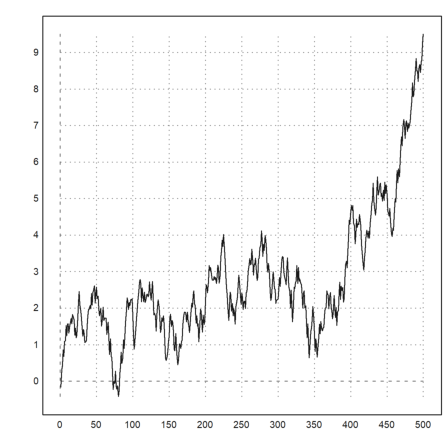
It is possible to use the wonderful plot library MatPlotLib from Euler. For this, MatPlotLib and NumPy must be installed for Python. This is done on the command line with
>python -m pip install -U pip >python -m pip install -U matplotlib
If you are using Anaconda for Python 2.7 these packages will be installed automatically. The following page contains some beginner tutorials to this library.
We need to import a few things in Python. We have to do this globally, since imports in functions are local.
>>> import matplotlib.pyplot as plt >>> import matplotlib.cm as cm
We write a function which does the plot. It does the following things.
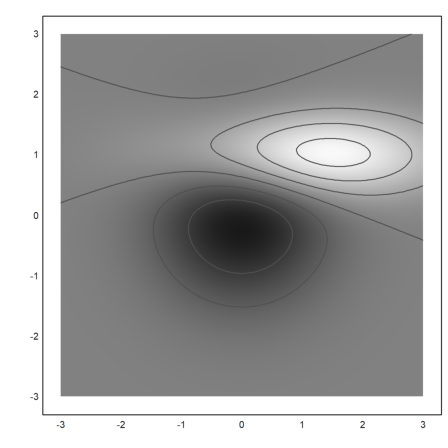
- Call figure() to set the size of the plot, - do the background shading with imshow(), - generate the contour lines with contour(), - generate labels for the contour lines.
>function python pycontour (X,Y,Z,a,b,c,d) ... plt.figure(figsize=[8,8]) plt.imshow(Z,interpolation='bilinear',origin='lower', cmap=cm.gray,extent=(a,b,c,d)) CS = plt.contour(X,Y,Z) plt.clabel(CS,inline=1,fontsize=10) endfunction
I took the code from the following page.
The arguments for plt.contour() include the X and Y vectors and a matrix of values Z=f(X,Y). In the demos, a numerical package for Python is used to generate these matrices. But we use EMT and pass the results to the Python function.
>x=-3:0.025:3; y=x; ... function qgauss(x,y,x0,y0,vx,vy) ...
## Two dimensional Gauß distribution return qnormal(x,x0,vx)*qnormal(y,y0,vy) endfunction
Now we compute the difference of two such distributions. And plot contour lines.
>Z1=qgauss(x,y',0,0,1,1); ... Z2=qgauss(x,y',1,1,1.5,0.5); ... Z=10*(Z2-Z1);
We can generate the plot and save it to a temporary file in the Euler working directory.
>pycontour(x,y,Z,-3,3,-3,3); pyins;
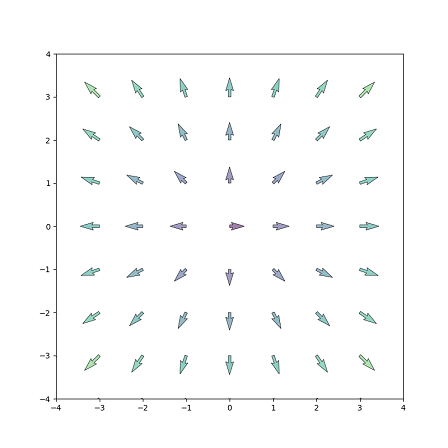
The function pyins() tells Python to generate an output file in PNG format and inserts this file into the notebook. The name of the output file is stored in the global variable pyout$$.
Its size depends on the parameter figsize= of figure(). The font is not scaled automatically. For EMT notebooks, [8,8] looks good. It generates an image of 800x800 pixels.
loadimg() can insert the file into the notebook. We reduce it to a height of about 10 lines of text.
>loadimg(pyout$$,10);
Here is the corresponding plot with Euler. Euler cannot do these nice labels without effort.
>plot2d(Z,r=3,levels=-3:0.5:3,>hue,grid=4):
After pyins() the plot is closed. But you can close all plots manually with plot.close('all').
>>> plt.close('all');
You can also use NumPy to compute the data of the plot in Python.
>>> import numpy as np
With this package we can define the following.
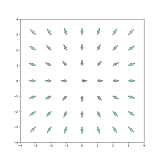
>function python pyvectors (n) ... X,Y = np.mgrid[0:n,0:n]-n/2.0 T = np.arctan2(Y, X) R = 10+np.sqrt(Y**2+X**2) U,V = R*np.cos(T), R*np.sin(T) plt.figure(figsize=[8,8]) plt.quiver(X,Y,U,V,R,alpha=0.5) plt.quiver(X,Y,U,V,edgecolor='k',facecolor='None',linewidth=0.5) plt.xlim(-n/2.0,n/2.0), plt.xticks([k-n/2.0 for k in range(0,n+1)]) plt.ylim(-n/2.0,n/2.0), plt.yticks([k-n/2.0 for k in range(0,n+1)]) endfunction
>pyvectors(8); pyins;
