This is a demonstration of the DLL feature in Euler. With DLLs, you can use C and even assembler code in Euler. Euler comes with the C compiler tinycc. You can compile files from the command line.
The following two lines are commented, since Euler cannot write to the installation directory. If you want to try the compilation, uncomment the lines and save the notebook to a directory with write access. For the source of the file, see
We copy the file to eulerhome(), which is usually "\Users\YourName\Euler". Compiling in the installation directory would cause an error.
>fn="Distribution of Primes.c"; filecopy(home()+fn,eulerhome()+fn); ... cd(eulerhome()); tccompile "Distribution of Primes";
The dll command loads the function dllprimes (which needs one parameter) from the DLL.
>dll("Distribution of Primes","dllprimes",1);
The function uses the sieve of Eratosthenes to compute all prime numbers up to a certain limit.
>dllprimes(100)
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
Let us try to find all prime numbers to 100 million.
>n=100000000;
tic and toc take the time. On my computer, it takes less than 3 seconds.
>tic; p=dllprimes(n); size(p), toc;
[1, 5.76146e+006] Used 1.584 seconds
It is interesting to plot the distribution of the primes. It is known that
![]()
where p[n] is the n-th prime number.
>k=1000:1000:cols(p); plot2d(k*log(p[k])/p[k],xl="*1000",>insimg);
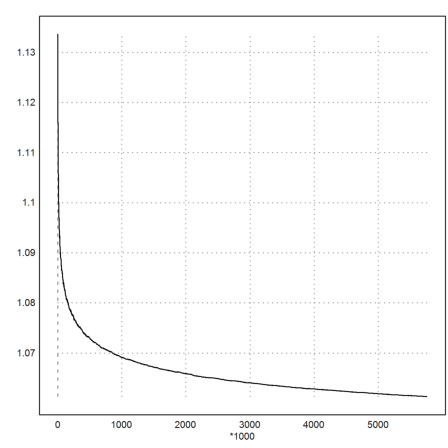
Usually this is stated in terms of the prime counting function
![]()
Then
![]()
But the above statement is equivalent, since n is the number of primes less than p[n]. For the function p[n] the following development is known
![]()
We check the O-constant.
>plot2d((p[k]/(k*log(k))-1-(log(log(k))-1)/log(k))*log(k)^2,xl="*1000"):
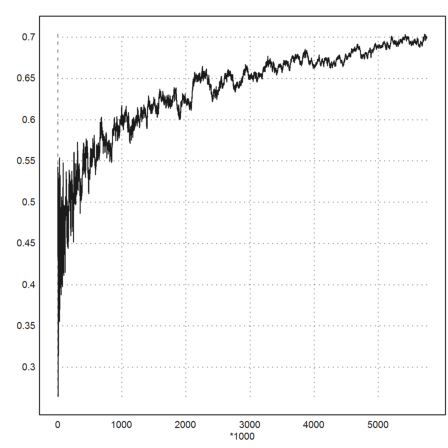
We can compute an approximation of the Meissel-Mertens constant.
>sum(1/p)-log(log(n))
0.261501242993
Or check Mertens second theorem. gamma$ is the Euler-Mascheroni constant.
>log(n)*prod(1-1/p), exp(-gamma$)
0.561457220953 0.561459483567
Euler has the sieve function. However, with the default stack size, only primes up to a million can be computed.
>tic; length(primes(100 000 000)), toc;
5761455 Used 1.966 seconds
The C code is faster, of course. The gain is a factor of 3.
>tic; length(dllprimes(100 000 000)), toc;
5761455 Used 1.53 seconds
Clearly, for other problems involving complicated data structures, Euler might be a completely wrong choice. Then the C interface is very nice. It can even keep data between subsequent calls.
The sieve function in Euler is straightforward coding in matrix languages, using an array for the odd numbers, and index arrays to avoid loops.
>type primes
function primes (n: integer)
if n>=3
len = floor((n-1)/2);
sieve = ones ([1,len]);
for i=1 to (sqrt(n)-1)/2;
if (sieve[i]) then
sieve[3*i+1:2*i+1:len] = 0; ..
endif
end
return [2, 1+2*nonzeros(sieve)];
elseif n>=2
return 2;
else
return [];
endif
endfunction