It is a well known fact and it has been observed in many real life data that the first digit of the data is not distributed evenly among all possible first digits 1 to 9. Rather the observed distribution for the digit i is
![]()
This is called Benford's law.
To test this law, I stole stock data from an site, and listed the daily trade volume of their stock into a file.
>v=readmatrix("volumes.dat")';
Here are the first 100 values.
>v[1:200]
[544157, 544157, 156075, 11862, 265267, 1.71407e+006, 479429, 1.68337e+006, 22709, 130265, 42516, 41107, 6995, 149473, 191975, 62920, 42462, 39557, 63524, 16511, 865995, 48299, 69100, 109735, 86305, 84685, 237742, 122700, 153005, 137054, 73998, 18846, 55636, 68715, 23939, 16670, 149444, 129363, 290037, 6582, 187479, 8488, 26133, 81853, 26185, 25048, 80988, 213087, 881591, 3.18527e+006, 117500, 86400, 113609, 18719, 1.05462e+006, 1.77765e+007, 1.71189e+007, 650646, 1.47722e+006, 270910, 456247, 67000, 355126, 489772, 916030, 1859, 95172, 118442, 125030, 172168, 101264, 265043, 93265, 588767, 3.66473e+006, 2.10848e+006, 147272, 452850, 2.51024e+006, 129672, 599131, 1.17062e+006, 43360, 3.53408e+006, 2.15011e+006, 261405, 10500, 41615, 1.01669e+006, 127458, 226756, 101700, 2.7435e+006, 274591, 291125, 14340, 59780, 178830, 1.21082e+006, 128018, 856704, 378086, 664557, 405999, 828502, 335948, 576086, 604670, 134000, 83000, 654082, 812007, 639507, 3.24893e+006, 268568, 3.93623e+006, 9.15216e+006, 8.02835e+006, 1.8367e+006, 221005, 386657, 1.57159e+006, 68764, 58385, 896267, 30670, 5.0522e+006, 93478, 3.66215e+006, 279015, 5650, 726680, 136385, 106236, 490220, 304752, 1.52216e+006, 1.95674e+006, 1.97216e+006, ... ]
To find the first digit of a number in its decimal representation, we can use the following function.
>function fd(x) ... n=floor(log10(x)); return floor(x/10^n) endfunction
The expected distribution is the following.
>d=log10(2:10)-log10(1:9)
[0.30103, 0.176091, 0.124939, 0.09691, 0.0791812, 0.0669468, 0.0579919, 0.0511525, 0.0457575]
Let us plot the distribution of the first digits in our data versus the expected distribution.
>columnsplot(getmultiplicities(1:9,fd(v))/length(v)); ... plot2d(1:9,d,>add); ... plot2d(1:9,d,>points,>add); ... insimg;
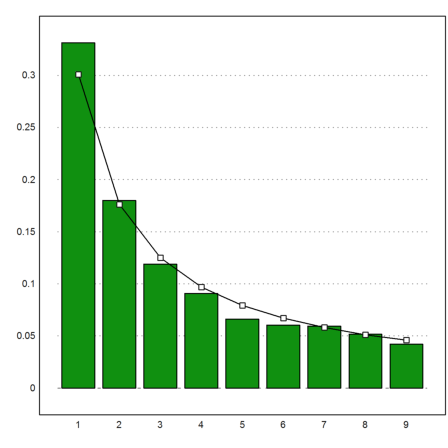
It is obvious that Benford's law is a better description of the reality than the assumption of an equal distribution.
Let us perform a statistical test to check the distribution. We first need the frequencies of the first digits in v.
>frequ=count(fd(v)-1,9)
[976, 530, 350, 267, 195, 178, 175, 152, 124]
With an equal distribution, we expect about 327 cases for each digit.
>nf=sum(frequ), fe=nf/9
2947 327.444444444
The chi-square test fails, of course.
>chitest(frequ,ones(1,9)*fe)
0
However, the chi-test fails also for our expected distribution, though not as badly as before.
>chitest(frequ,d*nf)
0.00887027918168
One could argue, that the distribution of the values is exponential. But this is not really the case. A logarithmic distribution of the random variable X would satisfy
![]()
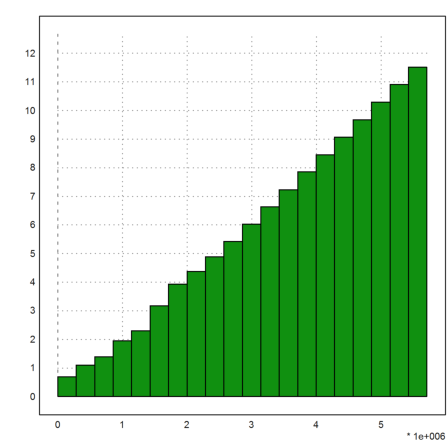
If we compute the logarithms for a cumulative frequency count of the values y, we see, that it is by no means linear.
>{x,y}=histo(v,20); plot2d(x,log(cumsum(flipx(y))),bar=true):

Let us compare this with an exponential distribution with the same mean value.
>m=mean(v)
469396.739396
The following Monte Carlo simulation produces such a distribution.
>vt=-log(random(1,100000))*m; mean(vt)
467459.444843
>{x,y}=histo(vt,20); plot2d(x,log(cumsum(flipx(y))),>bar):
Let us compare the distributing of the first digits we found in our sample with an exponential distribution. For this, we produce a sequence of first digits, which are distributed according to Benford's law.
>va=fd(10^random(1,nf));
We insert these into the same plot as above.
>columnsplot(getmultiplicities(1:9,fd(va))/length(va)); ... plot2d(1:9,d,>add); ... plot2d(1:9,d,>points,>add); ... insimg;
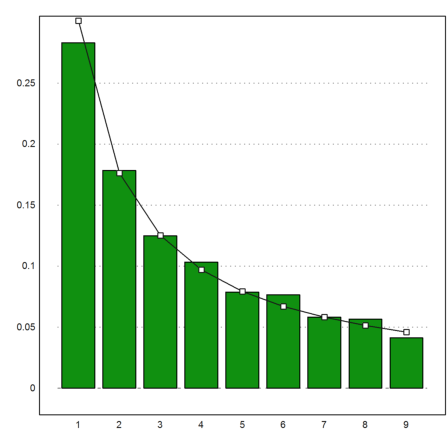
>frequa=count(fd(va)-1,9)
[834, 526, 368, 304, 232, 225, 171, 166, 121]
Most likely, the chi-square test cannot reject the distribution d for our Monte Carlo data.
>chitest(frequa,d*nf)
0.183718883574
A more general way to express Benford's law is to state that the fractions of the decadic logarithm of the data is distributed evenly in [0,1].
![]()
We can plot the distribution of these fractions for our data.
>plot2d(mod(log10(v),1),>distribution):
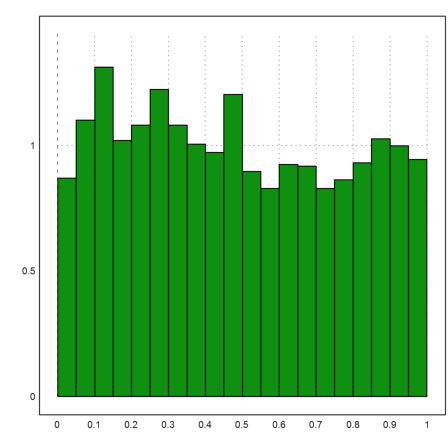
The result looks very good.