by R. Grothmann
In this notebook, we compute the formulas for the depth of field (DOF) of an ideal lens.
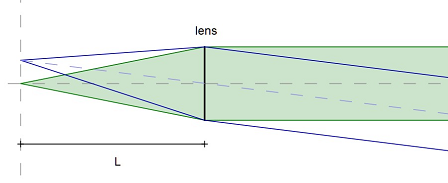
The image above shows, how parallel beams of light coming from a point at infinity are focussed at a distance L from the lens to the sensor.
In contrast, beams coming from a point at distance D will focus to a plane with distance X>L from the lens.
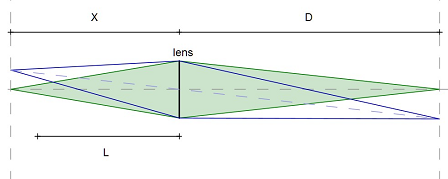
We derive the basic formula geometrically.
![]()
Here, L is the focal length, X is the distance of the film plane to the lens, and D is the distance of the object from the lens.
>beq &= 1/L=1/X+1/D
1 1 1
- = - + -
L X D
The geometric argument is in the following sketch. A light point in the upper right corner sends light beams out through the lens which are focussed at a distance X from the lens. We use the fact that we know two of the light beams. One goes through the center of the lens. The other goes rectangular onto the lens and meets the center axis at the focal length L of the lens.
Using similarity in the blue and gray triangle, we see
![]()
This yields the formula above with the notation of this notebook.
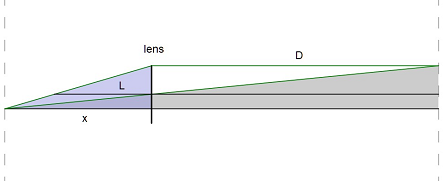
In the following function, X(D,L) is the distance of the film plane from the lens, such that an object in distance d is sharp.
>&solve(beq,X); function X(D,L) &= rhs(%[1])
D L
- -----
L - D
If a light point at distance DO is our object, its rays are within a cone behind the lens, focussing at X0 behind the lens. But the sensor is focussed for an object at distance D. So the intersections of the cone with the sensor is a circle. Let us call this the circle of diffusion.
The radius of this circle depends on the object distance DO, the focussed distance D, the focal length L, and the F-stop (aperture) A.
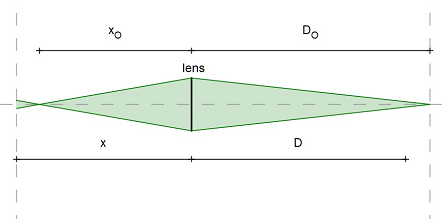
We can use a simple geometrical argument. Denote by X the distance of the film to the lens (for the set distance D), and XO the focus distance of the object at distance DO. Then the lens opening, which is be definition of the aperture equal to L/A, is multiplied by the factor
![]()
We get the following equation for this radius. For simplicity, we omit the absolute value which gives us negative values for DO>D.
Note, that D is always bigger than L. A camera cannot focus closer than the focal length.
We now define a function RD() which computes the radius of the circle of diffusion with the following parameters.
- object distance DO - focussed distance D - focal length L - aperture A
>function RD(DO,D,L,A) &= factor(ratsimp((X(DO,L)-X(D,L))/X(DO,L)*L/A))
2
(DO - D) L
------------
A DO (L - D)
For an example, let us plot the radius of diffusion for a 50mm lens, F8, set to a distance of 1m, for various object distances DO. Clearly, the image is sharp only if DO=D.
Don't forget, that we get negative radii, since we omitted the absolute value. Thus, we used the absolute value for the plot.
>plot2d("abs(RD(x,1m,50mm,8)*1000)",0.5,2,xl="DO",yl="r (mm)",>smaller):
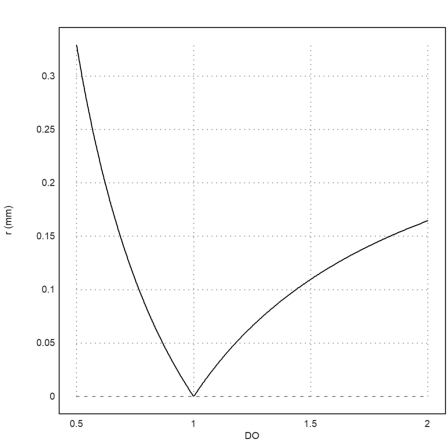
This is the blurriness of points at infinity. It depends on the focal length L, the aperture A and the focussed distance D.
![]()
>function RDINF(D,L,A) &= factor(limit(RD(DO,D,L,A),DO,inf))
2
L
---------
A (L - D)
Since D is usually much larger than L, we get a good approximation by
![]()
Shooting the same object at the same size with different focal lengths, we have to change the distance accordingly, so that L/D is constant. The blurriness is then proportional to L/A.
If your camera isn't a film size camera (aka "full frame"), it has a form factor (also called crop factor) ff. The form factor ff is 1 for 35mm (film), 1.5 for the DX format (1.6 for Canon), 2 for MFT, 4-5 for compact digital, 6-7 for smartphones.
It is convenient to compute a "film equivalent" focal length and aperture.
- L*ff is called the "film equivalent focal length" - A*ff is the "film equivalent aperture".
The film equivalent focal length determines the angle of view for a crop camera. The film equivalent aperture is useful to compute the Bokeh or the depth of field.
We can now define a formula for the size of the Bokeh. We compute it as a fraction of the diameter of the circle of diffusion by the diameter of the sensor.
The parameters are.
- the focussed distance D - the film equivalent focal length F - the film equivalent aperture A - the crop factor ff (default ff=1)
>function Bokeh(D,F,A,ff=1) := -2*RDINF(D,F,A)/(sqrt(0.024^2+0.036^2)/ff)
For a test, let us take a 85mm at f/4 lens on full frame, focussed to 2m distance. The result shows that the Bokeh will be quite smooth with circles covering 4.4% of the diameter of the image.
>round(Bokeh(2m,85mm,4),3)->"%"
4.4%
An equivalent lens on MFT will be 42.5mm at f/4. The background blurriness is almost the same.
>round(Bokeh(2m,42.5mm,2,2),3)->"%"
4.3%
An approximation of this formula is the following.
![]()
Here, L is the focal distance in millimeter, D the object distance in meters. The result is the Bokeh in percent. Note, that we have to a use "film equivalent" focal length and aperture here. Then, the form factor does no longer matter.
>round(85^2/(2*2)/400,1)+"%"
4.5%
The formula can help to judge the Bokeh for various lenses and cameras.
E.g., if you double the focal length (2*L) and back up for the same image (2*D), you get double the Bokeh.
For other cameras, you need to compute the film equivalent focal length and aperture first. E.g., an APS-C (ff=1.5) with 56mm focal length at F1.4 has the same Bokeh as our film camera above.
To get the near boundary of the DOF, we solve the equation, where the diameter of blur is equal to some largest admissable diameter. For 35mm this is usually taken as c=0.03mm. But we need to multiply this by the form factor ff, since the image will be magnified by this factor.
The function dn (near distance of DOF) will depend on the set distance d, the focal length together with the form factor, the F-stop a, and the maximal accepted radius c for film.
>function dn(D,L,A,c=0.03mm,ff=1) &= rhs(solve(RD(DO,D,L,A)=c/ff,DO)[1])
2
ff D L
---------------------
2
ff L - c A L + c A D
The same for the far end of the DOF.
>function df(D,L,A,c=0.03mm,ff=1) &= rhs(solve(RD(DO,D,L,A)=-c/ff,DO)[1])
2
ff D L
---------------------
2
ff L + c A L - c A D
As an example, we compute the DOF for 50mm film at F8, when the camera is set to 1m.
>[dn(1m,50mm,8),df(1m,50mm,8)]
[0.916422, 1.10035]
For a crop camera, the DOF will be smaller.
>[dn(1m,50mm,8,ff=1.5),df(1m,50mm,8,ff=1.5)]
[0.942685, 1.06474]
However, we have to take a lens with focal distance f/ff now to get a film equivalent focal length of f. Thus, we get a larger DOF.
>[dn(1m,50mm/1.5,8,ff=1.5),df(1m,50mm/1.5,8,ff=1.5)]
[0.877809, 1.16171]
To get an equivalent DOF, we use the film equivalent aperture A/ff..
>[dn(1m,50mm/1.5,8/1.5,ff=1.5),df(1m,50mm/1.5,8/1.5,ff=1.5)]
[0.915081, 1.10229]
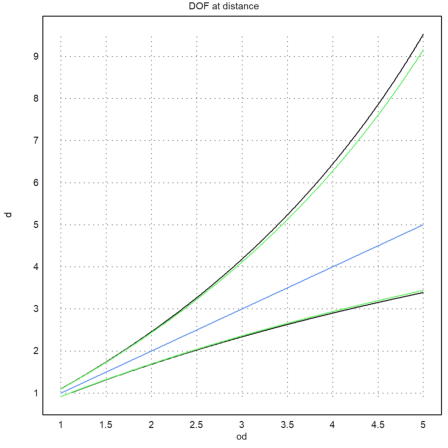
Let us plot the DOF for distances from 1m to 5m, 50mm, film, at F8.
>x=1:0.01:5; ... plot2d(x,dn(x,50mm,8)_df(x,50mm,8),xl="od",yl="d");
We add the DOF for a DX camera with a true focal length of 35mm. It is much wider if we use the same aperture, but about the same if we use an aperture of a=5.6.
>plot2d(x,dn(x,35mm,5.6,ff=1.5)_df(x,35mm,5.6,ff=1.5),>add,color=11);
The plot does also show that there is always more DOF behind the object, but not always twice as much, as a wide-spread rule of thumb says.
>plot2d(x,x,>add,color=12,title="DOF at distance"):
Let us make a function, which returns both ends of the DOF. The function will use the following parameters.
- focussed distance D. - film equivalent focal length L. - film equivalent aperture A. - acceptable blurriness c=0.03mm by default - ff=1 by default.
>function DOF(D,L,A,c=0.03mm,ff=1) ... dof = [dn(D,L/ff,A/ff,=c,=ff),df(D,L/ff,A/ff,=c,=ff)]; dof = max(dof,0); return dof endfunction
A few examples. First, a film camera with a 18mm, 35mm, 85mm lens at F8 set to 4m of distance. A zero at the upper end means sharpness to infinity.
>for L=[28mm,35mm,50mm,85mm]; DOF(4m,L,8), end;
[1.80512, 0] [2.25122, 17.9225] [2.90023, 6.4433] [3.53967, 4.59796]
Let us do the same for a camera with crop factor 1.5 at F5.6. We get very similar results.
>for L=[28mm,35mm,50mm,85mm]; DOF(4m,L,5.6*1.5), end;
[1.75692, 0] [2.20306, 21.6987] [2.8609, 6.64628] [3.51942, 4.63258]
Note that the true focal lengths are different for a DX camera. They have to be divided by the form factor.
>round([28mm,35mm,50mm,85mm]/1.5 -> mm)
[19, 23, 33, 57]
Here is the exact formula for the DOF in front of the focussed distance.
>&factor(D-dn(D,L/ff,A/ff,c,ff))
c A D (L - ff D)
- ------------------------
2
ff L - c A L + c ff A D
We want an approximation, which is easier to understand.
Now, L will be much smaller than ff*D, and c*A will be much smaller than L. Thus, the formula reduces to the following approximation, which does no longer depend on the form factor.
>&c*A*D^2/(L^2+c*A*D)
2
c A D
----------
2
L + c A D
If we divide by D^2, we get the following.
>&c*A/((L/D)^2+c*A/D)
c A
--------
2
L c A
-- + ---
2 D
D
To get the same image, we need to keep L/D constant. For large distances we see, that the DOF before the object depends only on the aperture A (besides the fixed c=0.03mm).
Let us try this exactly. As we see, the DOF is almost the same from 30mm to 150mm.
>plot2d("df(x/10,x/1000,4)-dn(x/10,x/1000,4)", ...
a=30,b=150,c=0,d=5,title="DOF at focal length, fixed object"):
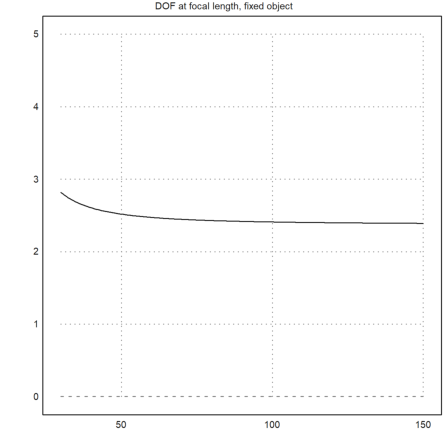
However, if we do this, the Bokeh at infinity increases with the focal length. Since F/D is constant, it increases with the focal length as shown in the section above.
But is cheaper and more effective to increase the focal length than to buy faster lenses, if the aim is to blur the background. There will also be less background in the image showing less distracting elements.
Next we compute the hyperfocal distance (HFD). This is the distance we have to focus at to get as much as possible DOF, ending at infinity.
First, we find an equation for the distance, such that the far end of the DOF is s.
>sequ &= solve(df(D,L,A,c,ff)=s,D)
2
ff s L + c s A L
[D = -----------------]
2
ff L + c s A
Now we take the limit as s approaches to infinity.
>function hfd(L,A,c=0.03mm,ff=1) &= limit(rhs(sequ[1]),s,inf)
2
ff L + c A L
-------------
c A
Again, we define a function HFD which depends on film equivalent numbers.
>function HFD(L,A,c=0.03mm,ff=1) := hfd(L*ff,A*ff,c)
E.g., at 50mm film, F8, we have to focus at 10.47m.
>round(HFD(50mm,8),2)
10.47
With a wide angle 28mm lens, we can focus much closer, and still get everything to infinity into DOF.
>round(HFD(28mm,8),2)
3.29
The exact formula for the hyperfocal distance, including the form factor, is the following.
>&factor(hfd(L/ff,A/ff,c,ff))
L (ff L + c A)
--------------
c ff A
Dividing by ff above and below, we get the following good approximation.
![]()
Again, L denotes the film equivalent focal length in millimeter.
>round(50^2/(30*8),2)
10.42
We need to know, where the DOF starts, if we use the hyperfocal distance. It is a fact that it starts at 1/2 of the HFD. As a rule, we have to focus on double the distance we want the DOF to start at.
>&ratsimp(hfd(L,A,c,ff)/dn(hfd(L,A,c,ff),L,A,c,ff))
2
We now can plot the HFD depending on the focal length for film format at F8.
>plot2d("HFD(x/1000,8)",a=18,b=120,c=0,d=70, ...
title="HFD at focal length (F8)", ...
xl="focal length in mm",yl="Hyperfocal distance in m"):
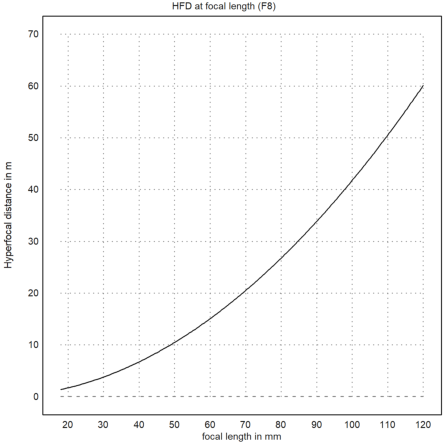
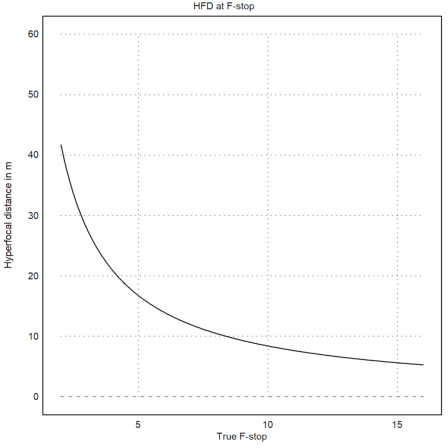
Or we can plot the HFD for 50mm for various F-stops. Clearly, we need to use higher F-stops, if we want more DOF.
>plot2d("HFD(50mm,x)",a=2,b=16,c=0,d=60, ...
title="HFD at F-stop", ...
xl="True F-stop",yl="Hyperfocal distance in m"):
There is a utility file containing these definitions.
>load dof
Functions for DOF, hyperfocal distance and Bokeh. startDOF, endDOF: computes depth of field (DOF) DOF: prints ranges of DOF hyperfocal: computes hyperfocal distance bokeh: computes quality of Bokeh (blurriness at infinity) lens: prints various parameters for a specific lens For another calculator: https://www.photopills.com/calculators/dof
For a portrait lens.
>lens(2m,85mm,2)
35mm equival focal length : 85.0 mm 35mm equival F-stop : F 2.0 Focussed distance : 2.0 m Start of DOF : 1.97 m End of DOF : 2.03 m Total DOF : 0.06 m Hyperfocal distance : 120.5 m Sharpness from : 60.3 m Bokeh quality : 8.7%
For landscape photography.
>lens(10m,28mm,13)
35mm equival focal length : 28.0 mm 35mm equival F-stop : F 13.0 Focussed distance : 10.0 m Start of DOF : 1.7 m End of DOF : infinity Hyperfocal distance : 2.0 m Sharpness from : 1.0 m
For a group of people, using an MFT camera.
>lens(6m,20mm,4,ff=2)
Crop factor : 2.00 True focal length : 20.0 mm 35mm equival focal length : 40.0 mm F-stop : F 4.0 35mm equival F-stop : F 8.0 Focussed distance : 6.0 m Start of DOF : 3.16 m End of DOF : 58.25 m Total DOF : 55.09 m Hyperfocal distance : 6.7 m Sharpness from : 3.3 m Bokeh quality : 0.2%
You can compare these values to