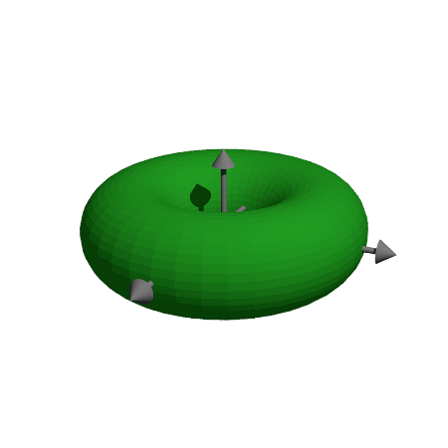
First let us make a really nice donat. We use Povray for that with Phong shading. These commands work only, if you have installed Povray properly.
>load povray; >povstart(angle=0,height=40°);
The following is a function to make donats.
>function povdonat (r1,r2,look="") := "torus {"+r1+","+r2+look+"}";
>writeln(povobject(povdonat(1,0.5),povlook(red,>phong),xrotate(90°)));
>povend();

The torus is the image of a cylinder under the following mapping.
>function phi(x,t,z) &= [x*cos(t),x*sin(t),z]
[cos(t) x, sin(t) x, z]
For Euler, we need the x-, y-, and z-coordinates of this mapping.
>function phix(x,t,z) &= phi(x,t,z)[1]; >function phiy(x,t,z) &= phi(x,t,z)[2]; >function phiz(x,t,z) &= phi(x,t,z)[3];
Now we generate a cylinder with a circle centered at x=R, y=0, z=0 of height 2pi.
>s=linspace(0,2pi,40); t=s'; >R=1; r=0.5; >x=R+r*cos(s); y=t; z=r*sin(s); >pov3d(x,y,z,zoom=4);

The transformation phi maps this cylinder to the donat. Each point is mapped with phi.
>X=phix(x,y,z); Y=phiy(x,y,z); Z=phiz(x,y,z); >pov3d(X,Y,Z,zoom=3.8);
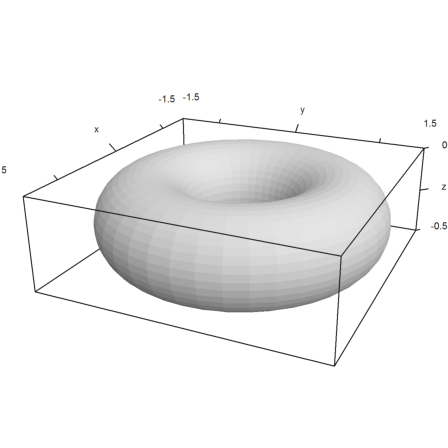
Here is the same image in Euler. We take -Z, since the default Euler shading is based on the correct side of the surface.
>plot3d(X,Y,-Z,>hue,zoom=3.6):
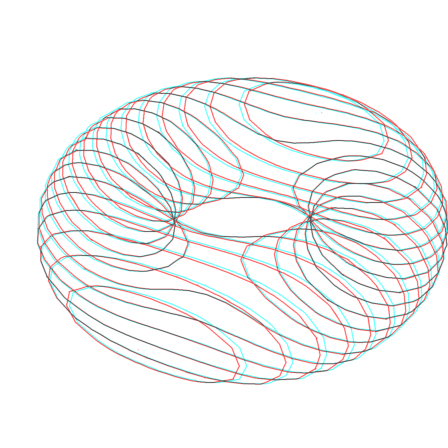
The following image is an Anagylph for red/cyan glasses showing the wire frame of torus with less details
>s=linspace(0,2pi,10); t=s'; ... R=1; r=0.5; ... X=phix(R+r*cos(s),t,r*sin(s)); ... Y=phiy(R+r*cos(s),t,r*sin(s)); ... Z=phiz(R+r*cos(s),t,r*sin(s)); ... plot3d(X,Y,Z,>wire,zoom=5,<frame,>anaglyph):
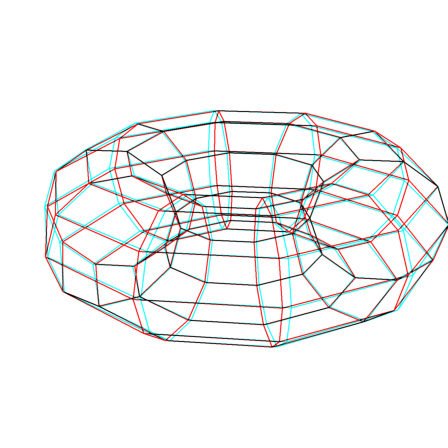
You need red/cyan glasses to appreciate the image.
The volume of a Donat can be computed with the Pappus' centroid theorem. It states for an area A in a plane rotated around one axis, which does not intersect the area and is in the same plane, that
![]()
where A is the area, and d is the length of the circle which the center of gravity of A travels along at one rotation.
For the donat with major radius 1 and minor radius 1/2, we rotate the following area A.
>t=linspace(0,2pi,100); ...
plot2d(1+cos(t)/2,sin(t)/2,>filled,r=2); ...
ctext("A",toscreen(1,0)); ...
plot2d(-1+cos(t)/2,sin(t)/2,>filled,>add,style="O",r=2); ...
insimg;
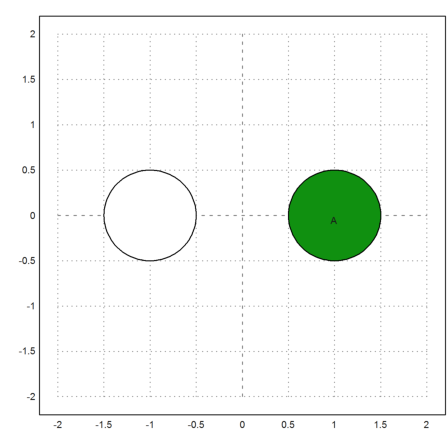
With major radius R and minor radius r, we get
![]()
Pappus' formula can be derived by elementary means, if we think of a small element dA of the area A at radius r. Rotating it yields a small tube of volume
![]()
Summing up, we see that we have to integrate r over A, which is equal to the mean value of r on A. Indeed
![]()
is the x-coordinate of the center of gravity of A.
>2*pi^2*1*0.5^2
4.93480220054
Using the transformation formula
![]()
is also easy. In fact the determinant is equal to x.
>&jacobian(phi(x,y,z),[x,y,z]), &det(%)|trigreduce
[ cos(y) - x sin(y) 0 ]
[ ]
[ sin(y) x cos(y) 0 ]
[ ]
[ 0 0 1 ]
x
So we have to integrate x over the cylinder.
![]()
The surface of the Torus can be computed with the second theorem of Pappus.
![]()
where L is the length of path around A, and sc is the center of gravity of the path. For our Torus we get
![]()
>4*pi^2*1*0.5
19.7392088022
For a Torus (like for a sphere) changing the minor radius by some small value dr changes the Volume by Sdr. Thus the surface is the derivative of the Volume to r.
>&diff(2*pi^2*R*r^2,r)
2
4 pi r R
We like to cut the donat with planes y=c, and to study these cuts.
The following commands call Povray to produce a sliced version of our donat.
>povstart(angle=0°,height=40°,light=[0,-0.1,1],zoom=3.6);
First the donat.
>donat=povobject(povdonat(1,0.5),xrotate(90°));
Now we define a function, which produces the cylinders for the cut.
>function cut(y1,y2) := povcylinder([0,y1,0],[0,y2,0],2);
Now a vector for the cuts.
>a=linspace(-1.5,1.5,21);
The cutting cylinders are stored in a vector of strings.
>s=[]; for i=1 to (length(a)-1)/2; s=s|cut(a[2*i],a[2*i+1]); end;
Form the union of the cuts.
>cuts=povunion(s);
And write the donut minus the cuts to the file.
>writeln(povdifference(donat,cuts,povlook(red))); >povend();

We cannot do the same in Euler. But there is an implicit plot, which needs a formula for the surface of the donat. To derive this formula we compute the distance of a point to the center circle of the donat.
![]()
This must be equal to r.
>expr &= (sqrt(x^2+y^2)-R)^2+z^2-r^2
2 2 2 2 2
(sqrt(y + x ) - R) + z - r
>plot3d(expr,implicit=1,r=1.5,<frame,zoom=5,>user,title="Turn the image"):

For the following, you need your red/cyan glasses again.
>plot3d(expr,implicit=1,r=1.5,<frame,zoom=5,height=40°,n=20,>anaglyph):
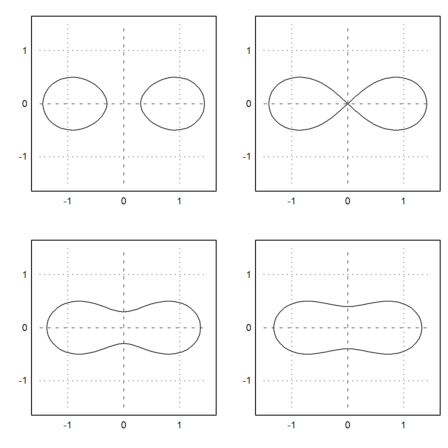
For the implicit plots of the cuts, we need to substitute y=c and then transform with z=y into the x-y-plane.
>expr1 &= expr with y=c with z=y
2 2 2 2 2
(sqrt(x + c ) - R) + y - r
Here are some cuts for y=0.4,0.5,0.6,0.7.
>figure(2,2); ... for k=1:4; figure(k); plot2d(&expr1 with c=0.3+k*0.1,r=1.5,level=0); end; ... figure(0):