Heron Formula
by R. Grothmann
We compute the area of a triangle with sides a, b and c. First set points into (0,0), (a,0) and (x,y), which form such a triangle. I.e., we solve
![]()
for x and y.
>sol &= solve([x^2+y^2=b^2,(x-a)^2+y^2=c^2],[x,y])
2 2 2
- c + b + a
[[x = --------------, y =
2 a
4 2 2 2 2 4 2 2 4
sqrt(- c + 2 b c + 2 a c - b + 2 a b - a )
- --------------------------------------------------],
2 a
2 2 2
- c + b + a
[x = --------------, y =
2 a
4 2 2 2 2 4 2 2 4
sqrt(- c + 2 b c + 2 a c - b + 2 a b - a )
--------------------------------------------------]]
2 a
Extract the solution y.
>ysol &= y with sol[2][2]
4 2 2 2 2 4 2 2 4
sqrt(- c + 2 b c + 2 a c - b + 2 a b - a )
--------------------------------------------------
2 a
We get the Heron formula.
>function F(a,b,c) &= sqrt(factor((ysol*a/2)^2))
sqrt((- c + b + a) (c - b + a) (c + b - a) (c + b + a))
-------------------------------------------------------
4
Of course, each rectangular triangle is a well known case.
>F(3,4,5)
6
And it is also obvious, that this is the triangle with maximal area and the two sides 3 and 4.
>plot2d(&F(3,4,x),1,7):
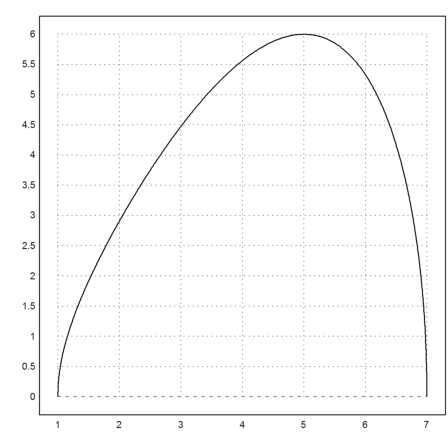
The general case works too.
>&solve(diff(F(a,b,c)^2,c)=0,c)
2 2 2 2
[c = - sqrt(b + a ), c = sqrt(b + a ), c = 0]
Now let us find the set of all points where b+c=d for some constant d. It is well known that this is an ellipse.
>s1 &= subst(d-c,b,sol[2])
2 2 2
(d - c) - c + a
[x = ------------------, y =
2 a
4 2 2 2 2 4 2 2 4
sqrt(- (d - c) + 2 c (d - c) + 2 a (d - c) - c + 2 a c - a )
--------------------------------------------------------------------]
2 a
And make functions of this.
>function fx(a,c,d) &= rhs(s1[1]), function fy(a,c,d) &= rhs(s1[2])
2 2 2
(d - c) - c + a
------------------
2 a
4 2 2 2 2 4 2 2 4
sqrt(- (d - c) + 2 c (d - c) + 2 a (d - c) - c + 2 a c - a )
--------------------------------------------------------------------
2 a
Now we can draw the set. The side b varies from 1 to 4. It is well known that we get an ellipse.
>plot2d(&fx(3,x,5),&fy(3,x,5),xmin=1,xmax=4,square=1):
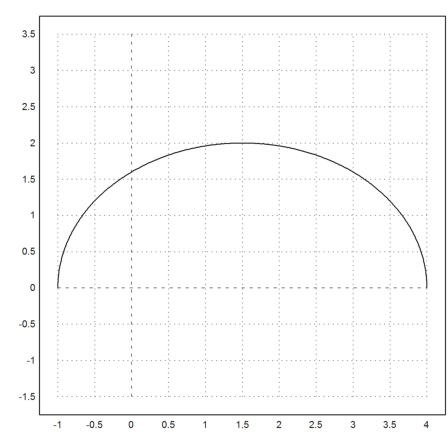
We can check the general equation for this ellipse, i.e.
![]()
where (xm,ym) is the center, and u and v are the half axes.
>&ratsimp((fx(a,c,d)-a/2)^2/u^2+fy(a,c,d)^2/v^2 with [u=d/2,v=sqrt(d^2-a^2)/2])
1
We see that the height and thus the area of the triangle is maximal for x=0. Thus the area of a triangle with a+b+c=d is maximal, if it is equilateral. We wish to derive this analytically.
>eqns &= [diff(F(a,b,d-(a+b))^2,a)=0,diff(F(a,b,d-(a+b))^2,b)=0]
d (d - 2 a) (d - 2 b) (- d + 2 b + 2 a) d (d - 2 b)
[--------------------- - ----------------------------- = 0,
8 8
d (d - 2 a) (d - 2 b) (- d + 2 b + 2 a) d (d - 2 a)
--------------------- - ----------------------------- = 0]
8 8
We get some minima, which belong to triangles with one side 0, and the solution a=b=c=d/3.
>&solve(eqns,[a,b])
d d d d
[[a = -, b = -], [a = 0, b = -], [a = -, b = 0],
3 3 2 2
d d
[a = -, b = -]]
2 2
There is also the Lagrange method, maximizing F(a,b,c)^2 with respect to a+b+d=d.
>&solve([diff(F(a,b,c)^2,a)=la,diff(F(a,b,c)^2,b)=la, ...
diff(F(a,b,c)^2,c)=la,a+b+c=d],[a,b,c,la])
d d d d
[[a = 0, b = -, c = -, la = 0], [a = -, b = 0, c = -, la = 0],
2 2 2 2
3
d d d d d d
[a = -, b = -, c = 0, la = 0], [a = -, b = -, c = -, la = ---]]
2 2 3 3 3 108
We can make a plot of the situation with the utility functions in geometry.e.
>load geometry;
First set the points in Maxima.
>A &= at([x,y],sol[2])
2 2 2
- c + b + a
[--------------,
2 a
4 2 2 2 2 4 2 2 4
sqrt(- c + 2 b c + 2 a c - b + 2 a b - a )
--------------------------------------------------]
2 a
>B &= [0,0], C &= [a,0]
[0, 0]
[a, 0]
Then set the plot range, and plot the points.
>setPlotRange(0,5,-2,3); ...
a=4; b=3; c=2; ...
plotPoint(mxmeval("B"),"B"); plotPoint(mxmeval("C"),"C"); ...
plotPoint(mxmeval("A"),"A"):

Plot the segments.
>plotSegment(mxmeval("A"),mxmeval("C")); ...
plotSegment(mxmeval("B"),mxmeval("C")); ...
plotSegment(mxmeval("B"),mxmeval("A")):

Compute the middle perpendicular in Maxima.
>h &= middlePerpendicular(A,B); g &= middlePerpendicular(B,C);
And the center of the circumference.
>U &= lineIntersection(h,g);
We get the formula for the radius of the circumcircle.
>&assume(a>0,b>0,c>0); & distance(U,B) | radcan
I a b c
---------------------------------------------------------------
sqrt(c - b - a) sqrt(c - b + a) sqrt(c + b - a) sqrt(c + b + a)
Let us add this to the plot.
>plotPoint(U()); ...
plotCircle(circleWithCenter(mxmeval("U"),mxmeval("distance(U,C)"))):
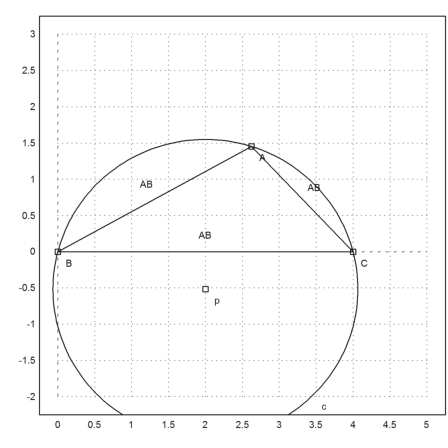
Using geometry, we derive the simple formula
![]()
for the radius. We can check, if this is really true with Maxima. Maxima will factor this only if we square it.
>& c^2/sin(computeAngle(A,B,C))^2 | factor
2 2 2
4 a b c
- -----------------------------------------------
(c - b - a) (c - b + a) (c + b - a) (c + b + a)