We solve
![]()
![]()
>function f([x,y]) &= [x^2+y^2-10,x+y-1]
2 2
[y + x - 10, y + x - 1]
Euler can plot the solutions of both equations.
>plot2d(&f(x,y)[1],level=0,r=5); ... plot2d(&f(x,y)[2],level=0,add=true):
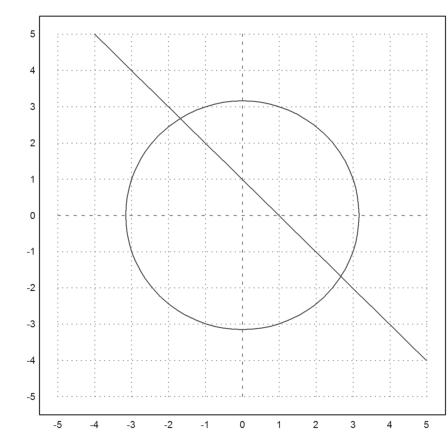
The intersections are the solutions.
To start the Newton algorithm we need the Jacobian.
>function Df([x,y]) &= jacobian(f(x,y),[x,y])
[ 2 x 2 y ]
[ ]
[ 1 1 ]
Now, there is the newton2 function, which does the iteration.
It needs to function f(v) and Df(v). That is, why we define f and Df with f([x,y]) and Df([x,y]). Those functions can be used with vectors or two elements.
>newton2("f","Df",[-3,3])
[-1.67945, 2.67945]
We want to simulate the Newton iteration step by step. So we define the iterating function.
>function fiter ([x,y]) &= [x,y]-invert(Df(x,y)).f(x,y)
[ 2 2 ]
[ - y - x + 10 2 y (y + x - 1) ]
[ -------------- + --------------- + x ]
[ 2 x - 2 y 2 x - 2 y ]
[ ]
[ 2 2 ]
[ y + x - 10 2 x (y + x - 1) ]
[ ------------ - --------------- + y ]
[ 2 x - 2 y 2 x - 2 y ]
>&factor(fiter(x,y))
[ 2 2 ]
[ - y + 2 y - x - 10 ]
[ -------------------- ]
[ 2 (y - x) ]
[ ]
[ 2 2 ]
[ y + x - 2 x + 10 ]
[ ------------------ ]
[ 2 (y - x) ]
Maxima returns a column vector. We need a row vector as input and output. So we define an iteration function g.
>function g(v) := fiter(v)'
Then we can iterate using the iterate() function.
>iterate("g",[-3.2,3],10)
-3.2 3
-1.87419 2.87419
-1.68744 2.68744
-1.67946 2.67946
-1.67945 2.67945
-1.67945 2.67945
-1.67945 2.67945
-1.67945 2.67945
-1.67945 2.67945
-1.67945 2.67945
-1.67945 2.67945
Another starting point yields the other solution.
>iterate("g",[1,-2],10)
1 -2
3.16667 -2.16667
2.72396 -1.72396
2.67989 -1.67989
2.67945 -1.67945
2.67945 -1.67945
2.67945 -1.67945
2.67945 -1.67945
2.67945 -1.67945
2.67945 -1.67945
2.67945 -1.67945
Of course, we can also solve this example symbolically.
>&solve(f(x,y)), %()
1 - sqrt(19) sqrt(19) + 1
[[y = ------------, x = ------------],
2 2
sqrt(19) + 1 1 - sqrt(19)
[y = ------------, x = ------------]]
2 2
[-1.67945, 2.67945, 2.67945, -1.67945]
There is also the Broyden algorithm, which does not need the derivative. It is a generalization of the Secant algorithm for more then one variable.
>broyden("f",[-3,2])
[-1.67945, 2.67945]
With the interval Newton method, we even get a proved inclusion of the zero.
>inewton2("f","Df",[-3,1])
[ ~-1.679449471770339,-1.679449471770335~, ~2.679449471770335,2.679449471770338~ ]