by R. Grothmann
We wish to cross a river swimming with speed v=1 m/s, the river floating with vr=4 m/s. The river is b=100 m wide.
>v=1; vr=4; b=100;
While we are swimming, we want to keep the same angle a to the coast of the river. The crossing speed (vertical to the cost) then reduces to
![]()
Let us first write a function, which computes the time it takes to cross the river.
>function t(a) := b/(sin(a)*v);
Then we write a function which computes the drift for the angle a. This is how much the river floats while we are crossing it, minus the length we are swimming upstream during that time. The speed parallel to the cost is
![]()
We must subtract this from the speed of the river to get our drifting speed. Multiplied by the time we take to cross the river, we get our drift.
>function drift(a) := t(a)*(vr-cos(a)*v);
We can plot the drift for various angles.
>plot2d("drift(rad(x))",a=1,b=90):
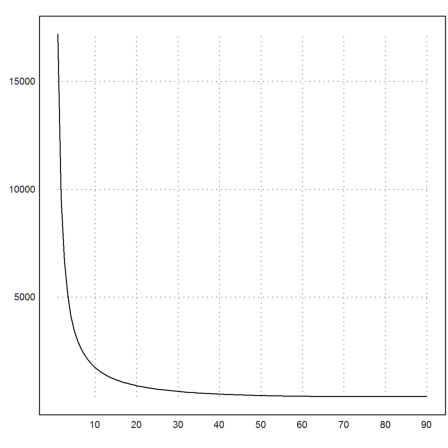
The angle of 0 would mean to swim parallel to the coast, which makes our crossing time infinite, and thus the drift.
There is an optimal angle with minimal drift between 70° and 80°.
>plot2d("drift(rad(x))",a=40,b=90):
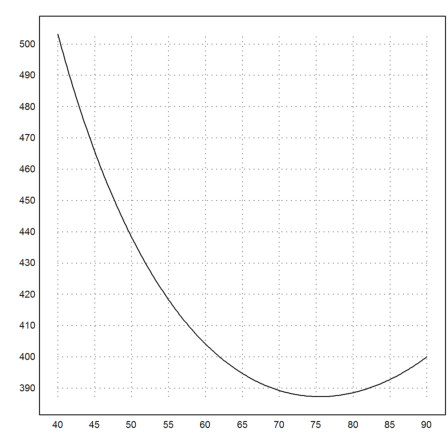
To compute this angle, we use fmin.
>shortformat; deg(fmin("drift",5°,90°))
75.5225
If the river is slower, we get a different optimal angle.
>vr=2; deg(fmin("drift",5°,90°))
60
Let us write a function to compute the optimal angle for any river speed.
Since we started with functions using global variables, we are forced to keep vr global. See below for a better approach.
>function opt (x) ...
global vr;
vr=x;
return fmin("drift",5°,90°);
endfunction
Plot this function.
>plot2d("deg(opt(x))",a=1,b=20); xlabel("River Speed vr"):
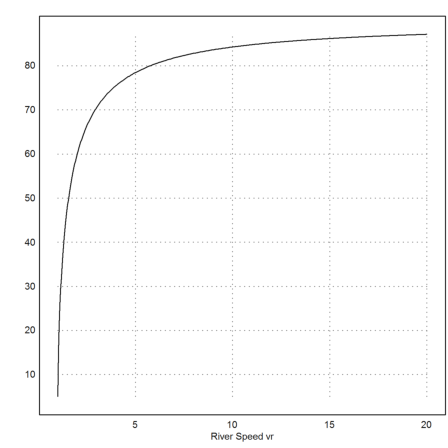
If the river speed goes to infinity, we must take the 90° angle, since then it becomes important to cross as fast as possible. If the river moves as slow as the swimmer, we need to go towards an angle of 0°, essentially swimming upstream. The drift then goes to 0.
If the river flows slower than the swimmer, we can reach any point on the opposite river bank.
To study the dependence of the optimal angle on v, vr or b, we define the following function, again using a lazy approach which modifies global variables.
>function opt3 (v1,vr1,b1) ...
global v,vr,b; v=v1; vr=vr1; b=b1;
return fmin("drift",1°,90°);
endfunction
It is quite clear that the optimal angle does not depend on b. Thus it does not help to change the angle during the crossover.
>deg(opt3(1,4,100)), deg(opt3(1,4,200)),
75.5225 75.5225
Due to scaling, the optimal angle will depend on v/vr only.
>deg(opt3(1,4,100)), deg(opt3(2,8,100)),
75.5225 75.5225
Now, let us find a symbolic solution for the problem.
>function drift(a) &= (vr-cos(a)*v)*b/(sin(a)*v)
b (vr - cos(a) v)
-----------------
sin(a) v
The derivative of this functions needs to be simplified with trigsimp.
>&trigsimp(ratsimp(diff(drift(a),a)))
b v - cos(a) b vr
-----------------
2
sin (a) v
Then the solver of Maxima finds a solution.
>&assume(v>0); &assume(vr>0); ... &solve(trigsimp(diff(drift(a),a))=0,a), &factor(drift(a) with %)
v
[a = acos(--)]
vr
2 2
b sqrt(vr - v )
----------------
v
We get for the optimal angle with minimal drift
![]()
>plot2d("deg(acos(v/x))",2,20):
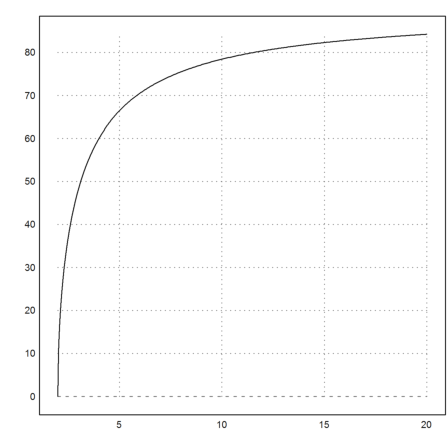
Assume we want to reach a point on the other side by walking with speed vd=2 after we climb out of the water. What is the optimal time for this?
We first reset our variables.
>v=1; vr=4; b=100;
Then we write a function, computing the total time it takes to cross the river. That is the swimmming plus the walking time. The point, we want to reach is d meters from the point of the exact other side downstream.
This time, we do not access global variables, but pass the location d and the walking speed vd as parameters.
>function totaltime(a,d,vd) := t(a)+abs(drift(a)-d)/vd
Lets us minimize this time choosing an optimal angle. We assume the point is 100m downstream.
>plot2d("totaltime(rad(x),100,2)",a=1,b=179):
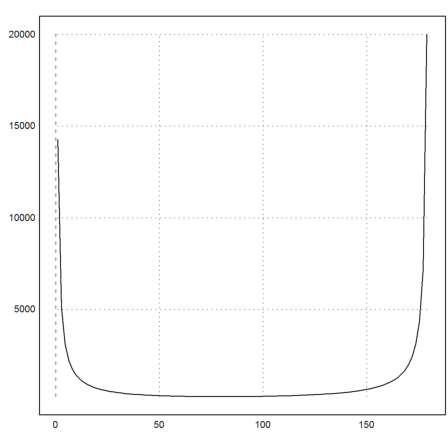
>plot2d("totaltime(rad(x),100,2)",a=45,b=120):
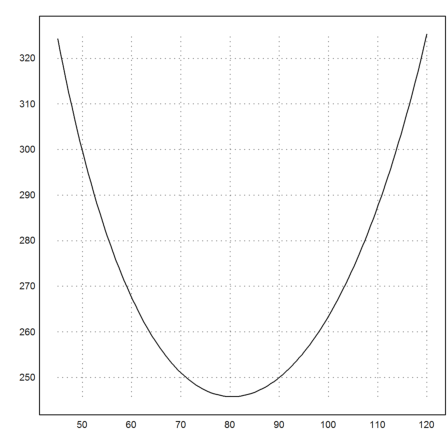
>amin=fmin("totaltime",1°,179°;100,2); deg(amin)
80.4059
>drift(amin)
388.771
Thus we have to swim, land 388m down the river, and walk back about 288m to our destination.
Surprisingly, the angle does not change with d for a long time.
>deg(fmin("totaltime",1°,179°;200,2))
80.4059
>deg(fmin("totaltime",1°,179°;300,2))
80.4059
The reason is the following: As long as we have to walk back, different distances d change the time only by a constant not depending on the angle of swimming. Thus, d does not matter for the optimal angle.
However, it is not optimal to choose the angle for minimal drift and then walk back. Instead, we must choose an angle that would be optimal for drift for a river with speed vr+vd. This follows from the formula (an exercise).
>vd:=2; deg(acos(v/(vr+vd)))
80.4059
When d becomes larger than 388.771 m, it is better to swim directly to the target.
>deg(fmin("totaltime",1°,179°;400,2))
90
>amin=fmin("totaltime",1°,179°;500,2); deg(amin)
117.019
We now swim directly to the destination.
>drift(amin)
500
If d tends to infinity, the angle will tend to 180°.
>amin=fmin("totaltime",1°,179°;800,2); deg(amin)
143.13
>drift(amin)
800
>amin=fmin("totaltime",1°,179°;8000,2); deg(amin)
176.418
>drift(amin)
8000
To investigate this, we write a function totalmin, that computes the minimal time for a distance d.
>function map totmin (d,vd) ...
return totaltime(fmin("totaltime",1°,179°;d,vd),d,vd);
endfunction
Let us plot this function. totalmin does not work for vectors. So we must use "map" to evaluate it for a vector d.
>d=0:10:1000; t=totmin(d,2); plot2d(d,t):
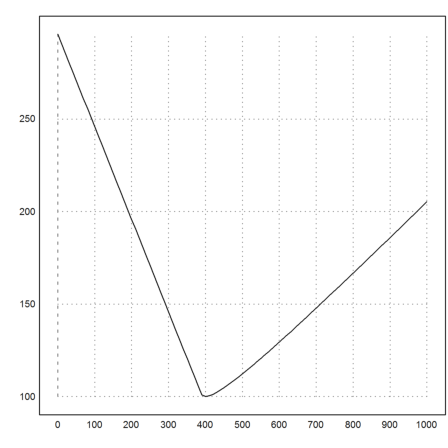
It looks, as if the function consists of two almost linear parts.
A closer plot confirms this.
>d=300:1:600; t=totmin(d,2); plot2d(d,t):
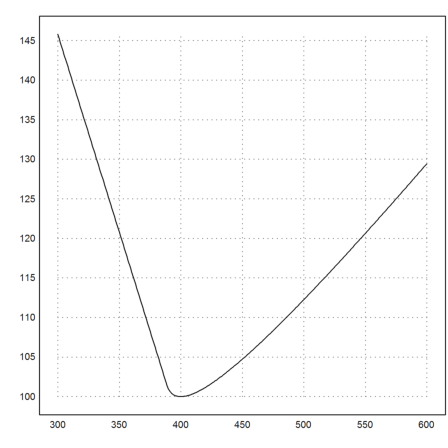
By the way, since our angle is larger than 90° now, it will not help to swim slower.
>v=1; totmin(500,2)
112.251
>v=0.9; totmin(500,2)
116.857